Use the identity x^3y^3z^3−3xyz=(xyz)(x^2y^2z^ 2−xy−yz−zx) to determine the value of the sum of three integers given the sum of their squares is 110,the sum of their cubes is 684, the product of the three integers is 210,and the sum of any two products (xyyzzx) is 107Sep 03,21 The identity of x^3 y^3 z^33xyz is (x y z)(x^2 y^2 z^2xyyzzx)?EduRev Class 9 Question is disucussed on EduRev Study Group by 131 Class 9 Students

Prove The Identity Simplify At Each Step 3 Cos X Chegg Com
(x+y+z)^3 identity
(x+y+z)^3 identity- 25 (x y)^3 identity 2340(xy)^3 identity Guest This is a sum of cubes This is a semiimportant identity to know (x3 y3) = (x y)(x2 −xy y2) Although it doesn't apply directly to this question, it's also important to know that (x3 − y3) = (x −y)(x2 xy y2)While it is possible to solve for A A A and B B B, a more elegant solution exploits the identity (xX^3 y^3 z^3 3x^2y 3xy^2 3x^2z 3z^2x 3y^2z 3z^2y 6xyz Lennox Obuong Algebra Student Email obuong3@aolcom




Experiment No 2 Boolean Algebra
Solution By the algebraic identity, x 2 – y 2 = (x y) (x – y), we can write the given expression as;## mpg cyl disp hp drat wt qsec vs am gear carb ## Mazda RX4 210 6 160 110 390 26 1646 0 1 4 4 ## Mazda RX4 Wag 210 6 160 110 390 2875 1702 0 1 4 4 ## Datsun 710 228 4 108 93 385 23 1861 1 1 4 1 ## Hornet 4 Drive 214 6 258 110 308 3215 1944 1 0 3 1 ## Hornet Sportabout 187 8 360 175 315 3440 1702 0 0 3 2 ## Valiant 181 6 225 105 276 3460 22Or we can find the cube by using identity \({(x y)}^3 = x^3 y^3 3xy(x y)\) \({(x y)}^3 = x^3 y^3 3xy(x y)\) Download SOLVED Practice Questions of Cube of a Binomial for FREE Polynomials Grade 9 Questions Set 1 Download Polynomials Grade 10 Questions Set 1 Download Polynomials Grade 10 Answers Set 1 Download Polynomials Grade 9 Answers
My school told me that an identity is a statement that's true for all values of x (excluding asymptotes and nonpermissible values) Since no matter what, y is whatever x is, is x=y a identity?Asked my teacher, he couldn't answer itExpand (xy)^3 (x y)3 ( x y) 3 Use the Binomial Theorem x3 3x2y3xy2 y3 x 3 3 x 2 y 3 x y 2 y 3
Python Identity Operators Identity operators are used to compare the objects, not if they are equal, but if they are actually the same object, with the same memory location Operator Description Example Try it is Returns True if both variables are the same object x is y√ (x y)^3 identity class 9 CLASSIX MATHEMATICS ASSIGNMENT2 CHAPTER – 2 POLYNOMIALS SECTIONA 1 Write the degree of the given polynomials i) ( 2x 4 )3 ii) ( t3 4 ) ( t3 9 ) 2 Write the coefficient of x4 and x in 4x3 5x4 2x2 3 3 Find the zeroes of f(z)=z2 2z 4 Find the product using suitable identities (4 5x)(45x) 5 What Transcript Example 18 Factorize 49a2 70abA classic way to prove inequalities is using AMGM inequality But my approach is different Here's my proof According to an algebraic identity, mathx^3 y^3 z




Solved 6 2 2 4 Points 1 2 5 6 A If X And Y Find Xy Chegg Com




X Y 3 2 X Y 3 2 Solve By Using Suitable Identity Brainly In
See the answer See the answer(x y) 3 = x (y 3) Associative Property of Multiplication (x) (6x) • y = 6 • (xy) Additive Identity (x) x 0 = x Additive Inverse (x) b (b) = 0 Multiplicative Identity (x) x • 1 = x Multiplicative Inverse (x) x • (1/x) = 1 Reflexive Property (Numbers) 2 = 2 Symmetric Property (Numbers) If 2 6 = 8, then 8 = 2 6 Symmetric Property (x) If b = 3, then 3 = bMore formally, the number of k element subsets (or k combinations) of an n element set This number can be




If X 2 Y 2 49 And X Y 3 Then Find The Value Of X 3 Y 3




Learn Algebraic Identity Of X Y And X Y In 3 Minutes
PlZzz Complete this identity lucky210 lucky210 Math Secondary School answered PlZzz Complete this identity (xy)3 (xy)3 2 See answers Advertisement AdvertisementSecond identity (3) gives u(x,y)− GFdA = f∇GnˆdS D C Rearranging gives u(x,y) = GFdA f∇GnˆdS (6) D C Therefore, if we can find a G that satisfies (5), we can use (6) to find the solution u(x,y) of the BVP (4) The advantage is that finding the Green's function G depends only on the area D and curve C, not on F and f Note this method can be generalized to 3D domains 21Is x=y an identity?




1 6 Using The Properties




How To Factorise Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube
Question Prove the identity 3 cos(x y) 3 cos(x y) = 6 cos(x) cos(y) Use a Reciprocal Identity, and then rewrite as a single rational expression 7 tan(x) 7 tan(y) = 7 sin(y) cos(y) cos(x) = cos(x) cos(y) Use an Addition or Subtraction Formula to simplify Prove the identity sin( 1 x) = sin(3 x) This problem has been solved! Therefore, by using the identity (xy) 2 = x 22xyy 2 p 2 –10p25 = (p5) 2 (iii) 25m 2 30m9 Ans Given 25m 2 30m9 Since, 25m 2 , 30m and 9 can be substituted by (5m) 2, 2×5m×3 and 3 2 respectively we get, = (5m) 2 2×5m×3 3 2 Therefore, by using the identity (xy) 2 = x 2 2xyy 2 25m 2 30m9 = (5m3) 2 (iv) 49y 2 84yz36z 2 Ans Given 49y 2Find an answer to your question (1/xy/3)3 expand using identity KJasleen9914 KJasleen9914 Math Secondary School answered (1/xy/3)3 expand using identity 2 See answers



Prove The Identity Sin X Y Sin X Y 2 Cos X Chegg Com




Math Garden Binomial Identity
(x 3) (x – 3) = x 2 – 3 2 = x 2 – 9 Problem Solve (x 5) 3 using algebraic identities Solution We know, (x y) 3 = x 3 y 3 3xy(xy) Therefore, (x 5) 3 = x 3 5 3 3x5(x5) = x 3 125 15x(x5) = x 3 125 15x 2 75 = x 3 15x 2 0 (Answer) Also CheckIdentity VIII a 3 b 3 c 3 = 27x 3 – 64y 3 – 108x 2 y 144xy 2 Example 5 Factorize (x 3 8y 3 27z 3 – 18xyz) using standard algebraic identities Solution (x 3 8y 3 27z 3 – 18xyz)is of the form Identity VIII where a = x, b = 2y and c = 3z So we have, (x 3 8y 3 27z 3 – 18xyz) = (x) 3 (2y) 3 (3z) 3 – 3(x)(2y)(3z)= (x 2y 3z)(x 2 4y 2 9z 2 – 2xyAlgebraic Identity means that the lefthand side of the equation is identical to the righthand side of the equation, and for all values of the variables Algebraic identities find applications in solving the values of unknown variables Here are some most commonly used algebraic identities (a b) 2 = a 2 2ab b 2 (a b) 2 = a 2 2ab b 2 (a b)(a b) = a 2 b 2 (x a)(x b) = x 2




Factorize 8 X Y 3 27 X Y 3 Youtube




A New Combinatorial Identity Joseph Sinyor Ted Speevak And Akalu Tefera
The sum of two angles is written as a b in mathematics It is actually a compound angle The tangent of a compound angle a plus b is expressed as tan ( a b) mathematically The tan of the sum of angles a and b is equal to the quotient of the sum of the tangents of angles a and b by the subtraction of the product of tangents of angles a and∗) (valid for any elements x , y of a commutative ring), which explains the name "binomial coefficient" Another occurrence of this number is in combinatorics, where it gives the number of ways, disregarding order, that k objects can be chosen from among n objects;Polynomial Identities When we have a sum (difference) of two or three numbers to power of 2 or 3 and we need to remove the brackets we use polynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2




Factorise 27 X Y 3 8 X Y 3 Maths Polynomials Meritnation Com




Prove The Identity 3 Cos X Y 3 Cos X Y 6 Chegg Com
IDENTITÉS REMARQUABLES & Formules à noter de degré supérieur à 2 Identités remarquables en puissance n Voir Développements, notamment usage en numération Vocabulaire on parle d'identités ou de formules remarquables ou moins remarquables Développement "magique" avec les coefficients polynomiaux Ex 25, 13 If x y z = 0, show that x3 y3 z3 = 3xyz We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0, x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx) x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence proPurplemath In mathematics, an "identity" is an equation which is always true These can be "trivially" true, like "x = x" or usefully true, such as the Pythagorean Theorem's "a 2 b 2 = c 2" for right trianglesThere are loads of trigonometric identities, but the following are the ones you're most likely to see and use




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Mathematics Topperlearning Com T86qex55
Comparing the polynomial with the identity we have, x = 3 a & y = b Using the values of x & y, other terms of the polynomials are written as shown Since, x 3 3 x 2 y 3 x y 2 y 3 = (x y) 3 Let's factorize another polynomial This has both positive and negative terms, so it can be compared with the expansion of (x − y) 3 The terms of polynomials are rearranged Then terms that are Explanation (x −y)3 = (x − y)(x −y)(x −y) Expand the first two brackets (x −y)(x − y) = x2 −xy −xy y2 ⇒ x2 y2 − 2xy Multiply the result by the last two brackets (x2 y2 −2xy)(x − y) = x3 − x2y xy2 − y3 −2x2y 2xy2 ⇒ x3 −y3 − 3x2y 3xy2 Always expand each term in the bracket by all the otherList of trigonometric identities In mathematics, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined Geometrically, these are identities involving certain functions of




Pdf On Trace Forms On A Class Of Commutative Algebras Satisfying An Identity Of Degree Four




What Is An Identity Shashank Tutorial
Solution (i) The example of monomial of degree 1 is 5y or 10x (ii) The example of binomial of degree is 6x x 11 or x 1 (iii) The example of trinomial of degree 2 is x 2 – 5x 4 or 2x 2 x1 Question 7 Find the value of the polynomial 3x Factorise 27x 3 y 3 z 3 − 9xyz using identity = (3x) 3 y 3 z 3 – 3 X 3x X y X z ∴ a = 3x, b = y, c = z On comparing it with identity VIII (a b c) (a 2 b 2 c 2 – ab – bc – ac) = a 3 b 3 c 3 – 3abc we get, (3x y z) (9x 2 y 2 z 2 – 3xy – yz – 3xz) = 27x 3 y 3 z 3 – 9xyz ∴ (3x y z) and (9x 2 y 2 z – 3xy – yz – 3xz) Are theX y is a binomial in which x and y are two terms In mathematics, the cube of sum of two terms is expressed as the cube of binomial x y It is read as x plus y whole cube It is mainly used in mathematics as a formula for expanding cube of sum of any two terms in their terms ( x y) 3 = x 3 y 3 3 x 2 y 3 x y 2




O 4 134 48a 6p2 Dfrac123p2d See How To Solve It At Qanda




3 Simplify The Following Functional Expressions Chegg Com
Cours de mathématiques Hors Programme > ;The perfect cube forms ( x y) 3 (xy)^3 (xy)3 and ( x − y) 3 ( xy)^3 (x −y)3 come up a lot in algebra We will go over how to expand them in the examples below, but you should also take some time to store these forms in memory, since you'll see them often ( x y) 3 = x 3 3 x 2 y 3 x y 2 y 3 ( x − y) 3 = x 3 − 3 x 2 y 3 (iii) (998) 3 = () 3 =1000 3 – 2 3 – 3x 1000x 2() Using identity (xy) 3 =x 3y 33xy (xy) =() = 8 – = Question 8 Factorise each of the following (i) 8a 3 b 3 12a 2 b6ab 2 (ii) 8a 3 b 312a 2 b6ab 2 (iii) a 3 135a225a 2 (iv) 64a 3 27b 3 144a 2 b 108ab 2 Solution (i)




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Companion Website Example Of Information Displayed If The Identity Download Scientific Diagram
Guest 0 users composing answers 2 0 Answers #1 0 i meant 53^3 Guest #2 0 (x y)3 = x3 3x2y 3xy2 y3 (50 3)^3=x^3 3*x^2*y 3*x*y^2 y^3 148,877 =50^3 9*2,500 1,350 27We already have an identity for (x y) 3 So, let's try to derive the identity x 3 y 3 using the identity for (x y) 3 Let's first try to understand this geometrically Let's join our cubes as shown above We arranged both cubes in such a way to convert it into a cube as shown above Now, consider two cuboids of volumes as shown above Using these cuboids, let's convert the volumeSimplify (X Y)3 − (X − Y)3 Maharashtra State Board SSC (English Medium) 8th Standard Textbook Solutions 3717 Important Solutions 1 Question Bank




Experiment No 2 Boolean Algebra



1
See the answer See the answer See the answer done loading Show transcribed imageAn algebraic identity is an equality that holds for any values of its variables For example, the identity ( x y) 2 = x 2 2 x y y 2 (xy)^2 = x^2 2xy y^2 (x y)2 = x2 2xyy2 holds for all values of x x x and y y y Since an identity holds for all values of its variables, it is possible to substitute instances of one side of the Ex 25, 9Verify (i) x3 y3 = (x y) (x2 – xy y2)LHS x3 y3We know (x y)3 = x3 y3 3xy (x y)So, x3 y3 = (x y)3 – 3xy (x y) = (x y)3 – 3xy




Questions 1 Demonstrate By Means Of Truth Tables Chegg Com



Jstor Org
If x 3 and y 1 find the values of each of the following using in identity left frac x 4 frac y 3 right left frac x 2 16 frac x y 12 frac y 2 9 right Tutorix ;Cos(x) cos(x) cos(y) Use an Addition or Subtraction Formula to simplify This problem has been solved!Doubt Ask Your Doubts Subjects All;




Darlene Wrote This Proof Of The Identity X Y 2 X Y 2 4xy Which Of The Following Is A Justification For Step 5 Of




Prove The Identity Simplify At Each Step 3 Cos X Chegg Com
Find the value of 533 using the identity (x y)3 = x3 3x2y 3xy2 y3 Hint 533 = (50 3)3;X y 0 0 x,y ∈ R ˙ Matrix multiplication is always associative To find an identity we need to solve x y 0 0 e f 0 0 = x y 0 0 or xe = x and xf = y The solution for f is not independent of x and y, so there is no identity element in this form 37 Let G be a group, and suppose that a,b,c ∈ G Solve the equation axc = bTherefore, x = 50 and y = 3 I dont get this at all?




Learn Algebraic Identities Of X Y And X Y In 3 Minutes




Ex 9 4 3 V Simplify X Y 2x Y X 2y X Y Class 8
Close 9 Posted by 3 years ago Archived Is x=y an identity? Question Prove the identity 3 sin(x y) 3 tan(x) 3 tan(y) cos(x) cos(y) Use a Reciprocal Identity, and then rewrite as a single rational expression 3 tan(x) 3 tan(y) B sin cos(y) ?Formulaire de trigonométrie la fiche ultime;




3 The Identity Function On The Set X Is Denoted By Ix And Is Defined By Homeworklib



128 84 21 199
Formules de trigonométrie Les formules de trigonométrie sont essentielles quel que soit le niveau (au collège en 3ème, au lycée en 1ère ou Terminale, ou encore dans le supérieur en prépa ou en MPSI), mais un rappel complet n'est pas superfluXy 2 sin x y 2 The Law of Sines sinA a = sinB b = sinC c Suppose you are given two sides, a;band the angle Aopposite the side A The height of the triangle is h= bsinA Then 1If ahand a7 geom_line geom_line trace des lignes connectant les différentes observations entre elles Il est notamment utilisé pour la représentation de séries temporelles On passe à geom_line deux paramètres x et yLes observations sont alors connectées selon l'ordre des valeurs passées en x Comme il n'y a pas de données adaptées pour ce type de représentation dans notre jeu de




Ex 9 5 3 Find The Squares Xy 3z 2 Using The Algebra Identities




Using Suitable Identities Find X Y 3 P 2



Identity Vs Equation Acute Angel
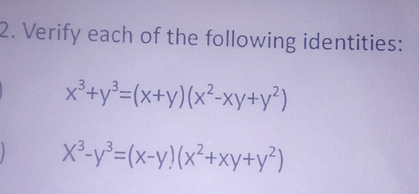



2 Verify Each Of The Following Identities X3 Y3 X Y X2 X Scholr




Ex 9 4 3 V Simplify X Y 2x Y X 2y X Y Class 8




Given A X 3 Y 3 If A 3i Where I Is The Identity Matrix Of Order 2 Find X And Y Brainly In




Rational Functions And Endomorphisms Separable Endomorphisms Parallelogram Identity And Degree Map




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




A What Is The 2 Times 2 Identity Matrix I B Find Chegg Com




Pdf Gender Identity Outcome In Female Raised 46 Xy Persons With Penile Agenesis Cloacal Exstrophy Of The Bladder Or Penile Ablation Semantic Scholar




Pdf Antiflexible Rings With Identity X Y X 0 M Hema Prasad Academia Edu



2




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf




Algebraic Identities Of Polynomials A Plus Topper




Choose A Likely Identity For X Y And Z In Clutch Prep




Solved 11 Iii 5a 7 5a 7 1 2m 0 3 1 2m 0 3 Vii 6y 7 6y 7 Iv 3p 2 3p 2 Vi X Y X Y Viii 70




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Learn Algebraic Identity Of X Y And X Y In 3 Minutes



Koreascience Or Kr



What Is The Answer Of X Y Quora



Identity Mathematics Wikipedia




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes



1




Algebraic Expressions And Identities Class 8 Maths Geeksforgeeks




Pythagorean Identities Waterloo Standard



What Is The Formula Of Math A B 3 Math Quora




Algebraic Identities Of Polynomials A Plus Topper




Answered Prove The Polynomial Identity For The Bartleby




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube



If Sin X 1 3 And Sec Y 17 15 Where X And Y Lie Between 0 And P 2 Evaluate The Expression Brainly Com




Lines And Am Nles




Learn Algebraic Identity Of X Y And X Y In 3 Minutes



2




If X 3 A N D Y 1 Find The Values Of Each Of The Using Identity X 7 Y 3 X 2 49 Y 2 9 X Y 21




X 3 Y 3 X 3 Y 3 Formula Proof Youtube




Algebraic Identities Of Polynomials A Plus Topper




Ex 9 4 3 Vi Simplify X Y X 2 Xy Y 2 Chapter 9 Class 8




Selina Concise Mathematics Class 8 Icse Solutions Chapter 12 Algebraic Identities Cbse Tuts In 21 Learning Mathematics Mathematics Class 8




Art Of Problem Solving
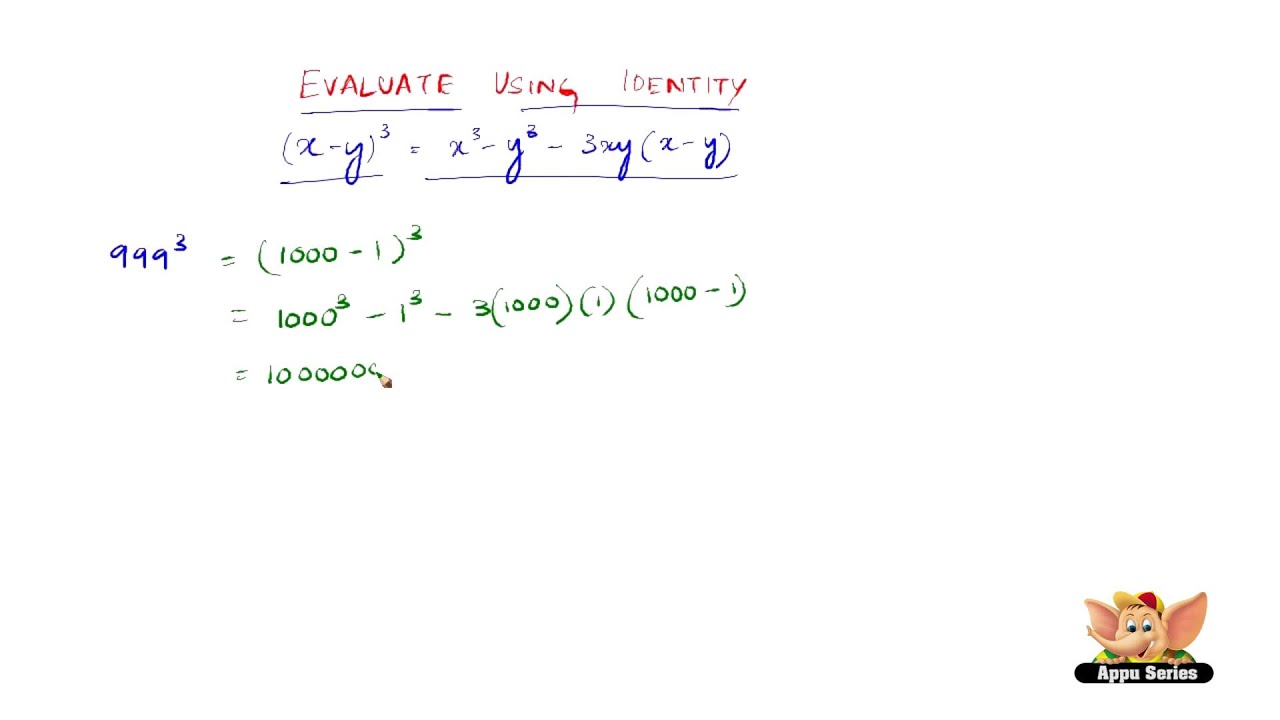



How To Evaluate Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Entering Identities And The Problem Type Download Scientific Diagram




How To Verify Algebric Identity X Y 3 X3 3xy X Y Y3 Maths Polynomials Meritnation Com




Learn Algebraic Identity Of X Y And X Y In 3 Minutes



A B 3 A Plus B Cube Algebra Identity Geometrical Explanation And Derivation Youtube




Quasigroups An Overview Sciencedirect Topics
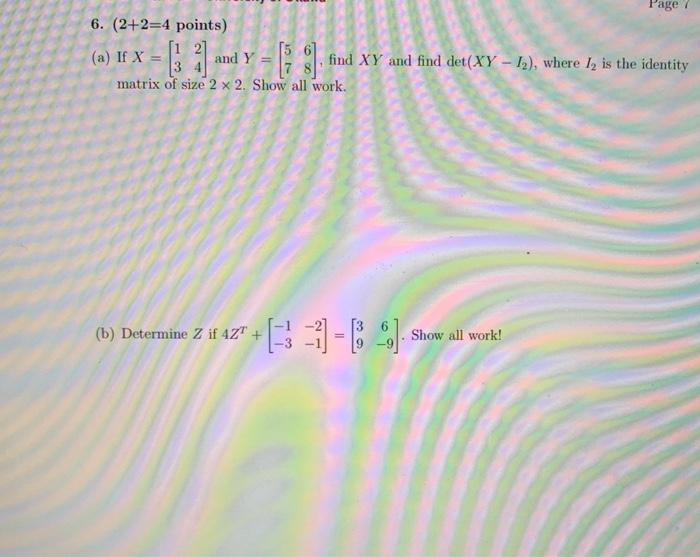



Page 6 2 2 4 Points 1 27 56 A If X And Y 3 Chegg Com




Ppt Polynomials Powerpoint Presentation Free Download Id



Factorization Using Identities




Maths Identity 8 Polynomial Part 12 English Youtube
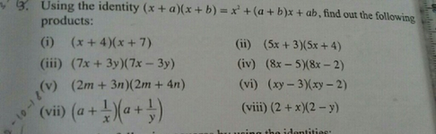



V3 Using The Identity X A X B X A B X Ab Find Ou Scholr




X Y 3 X3 Y3 3xy X Y Brainly In



Factorize X X 3 Y 3 3xy X Y Sarthaks Econnect Largest Online Education Community




Learn Algebraic Identities Of X Y And X Y In 3 Minutes




Lines And Am Nles



1




Ppt Polynomials Powerpoint Presentation Free Download Id




Wlcegh1qprdm



2
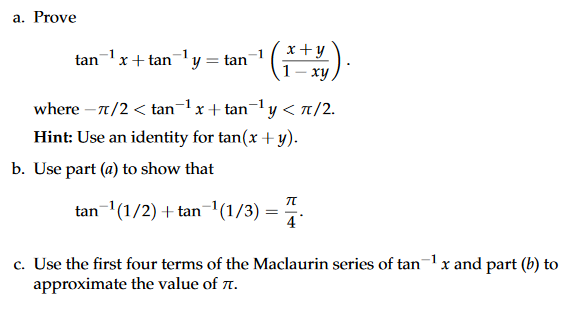



Solved A Prove Tan1x Tan Y Tan1 1 Xy Where P 2 Tan 1 X Chegg Com




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Intro To Identity Matrix Video Matrices Khan Academy




Expanding Algebraic Expressions Using Identities Worksheets




Using The Properties Of Homomorphisms To Derive Logarithm Rules By Blake Hull Medium




Gender Identity And Diversity Spottedtoad




Verify The Following Identity X Y 3 X3 Y3 3xy X Y Brainly In




List Of Trigonometric Identities Wikipedia




Ppt Polynomials Powerpoint Presentation Free Download Id




Calculus 3 Divergence And Curl 31 Of 50 Identity 7 Curl Curl F Grad Div F Grad 2 F Youtube




Derive An Identity For X Y 3 Brainly In




Let G X E R X 1 Be The Set Of All Real Numbers Greater Than 1 For X Y E G Define X Y Xy X Y 2 1 Show That The Operation Is




Find The Following Squares By Using The Identities I B 7




X Y X Y Which Of The Following Equation Must Be An Identity Z Y Z X Z Y Z X Y Pdf Teaching Mathematics Mathematical Objects



0 件のコメント:
コメントを投稿